Определение 1. Вектор г называется вектор-функцией скалярного аргумента t, если каждому значению скаляра из области допустимых значений соответствует определенное значение вектора г. Будем это записывать так: Если вектор г является функцией скалярного аргумента t то координаты х, у, z вектора г также будут функциями аргумента t: Вектор-функция скалярного аргумента. Годограф. Предел и непрерывность вектор-функции скалярного аргумента Обратно, если координаты вектора г являются функциями t% то функцией t будет и сам вектор г: Таким образом, задание вектор-функции r(f) равносильно заданию трех скалярных функций y(t), z(t). Определение 2. Годографом вектор-фун-кции r(t) скалярного аргумента называется геометрическое место точек, которое описывает конец вектора г(*) при изменении скаляра t, когда начало вектора r(f) помешено в фиксированную точку О пространства (рис. I). Годографом ради уса-вектора г = г(*) дви- Рис. 1 жушейся точки будет сама траектория L этой точки. Годографом скорости v = v(J) этой точки будет некоторая другая линия L\ (рис.2). Так, если материальная точка движется по окружности с постоянной скоростью |v| = const, то ее годограф скоростей также представляет собой окружность с центром в точке 0\ и с радиусом равным |v|. Пример 1. Построить годограф вектора г = ti + t\ + t\. Решение. 1. Это построение можно весги по точкам, составляя таблицу: Рис.3 2i Можн поступить и тйк. Обозначив через х, у, z координаты вектора V, будем иметь Нц И ключря из этих уравнений параметр 1У получим уравнения поверхностей у - z = х1, линия пересечения L которых и определит годограф вектора г() (рис.3). D> Задачи для самостоятельного решения. Построить годографы векторов: Пусть вектор-функция г = скалярного аргумента t определена в некоторой окрестности значения to аргумента t, кроме, быть может, амого значения доопределение 1. Постоянный вектор Л называется пределом вектора г(t) при, если для любого е > 0 существует б > 0 такое, что лля всех t ф to, удовлетворяющих условию 11 - выполняется неравенство Как и в обычном анализе, пишут limr(0=A. Рис.4 Геометрически это означает, что вектор) при t -* to стремится к вектору А как по длине, так и по направлению (рис.4). пределение 2. Вектор а(£) называется бесконечно малым при t -» to, если а(£) имеет предел при t -* to и этот предел равен улю: Вектор-функция скалярного аргумента. Годограф. Предел и непрерывность вектор-функции скалярного аргумента ли, что то же, для любого есуществует 6 > 0 такое, что для всех t Ф to, удовлетворяющих условию, выполняется неравенство |а(£)| ример 1. Показать, что вектор есть бесконечно алый вектор при t -* 0. Решение. Имеем ткуда видно, что если для всякого е 0 взять 6 = ~, то при -0| будем меть |. Согласно определению это означает, что a(t) есть бесконечно алый вектор при t 0. 1> адачи для самостоятельного решения г. Показать, что предел модуля вектора равен модулю его предела, если последний предел существует. . Доказать, что для того чтобы вектор-функция г(*) имела при to предел А, необходимо и достаточно, чтобы г(можно было представить в виде Вектор-функция скалярного аргумента. Годограф. Предел и непрерывность вектор-функции скалярного аргумента де a(t) - бесконечно маши при t -* t0 вектор. 14. Вектор-функиия а+ b(*) непрерывна при t = t0. Следует ли отсюда, что векторы a(t) и b(J) также непрерывны при t - to? 15. Доказать, что если a(- непрерывные вектор-функиии, то их скалярное произведение (a(*),b(f)) и векторное произведение |a(f),b(t)] также непрерывны.
Скачать с Depositfiles
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
I . ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
Вектор-функция (определение 1.1), способы её задания.
Радиус-вектор и годограф, параметрическое задание годографа.
Производная вектор-функции (определение 1.6).
Геометрический смысл производной вектор-функции.
Правила дифференцирования вектор-функций.
1.1. ОПРЕДЕЛЕНИЕ ВЕКТОР-ФУНКЦИИ
Определение 1.1
Если каждому значению скалярного аргумента
поставлен в соответствие вектор 
трехмерного пространства
R
3
, то говорят, что на множестве Х задана вектор-функция (или векторная функция) скалярного аргумента
t
.
Если в пространстве
R
3
задана декартова система координат
О
xyz
, то задание вектор — функции 
, 
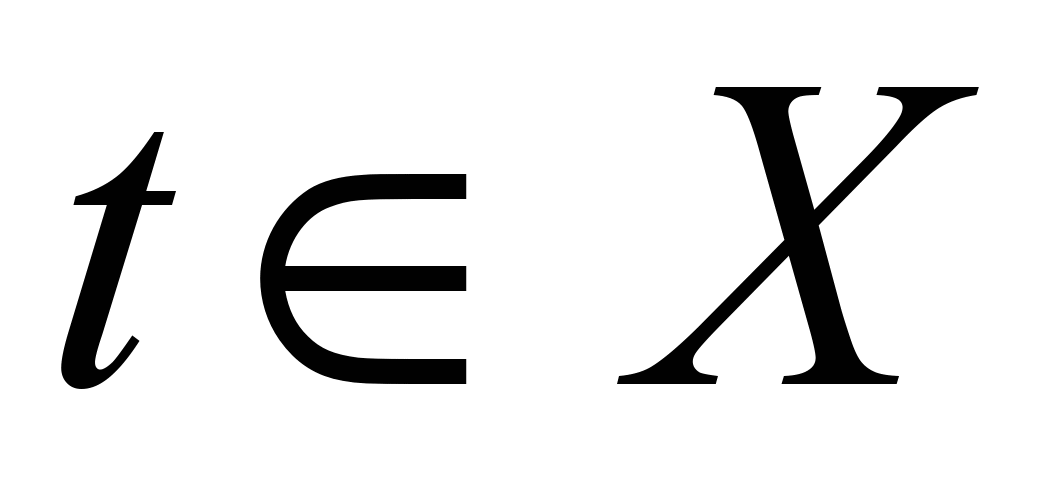равносильно заданию трех скалярных функций
х(
t
),
y
(
t
),
z
(
t
)
– координат вектора :
= { x ( t ), y ( t ), z ( t )} (1.1)
или , (1.2)
где 
— координатные орты.
1.2. ПРОСТРАНСТВЕННАЯ ЛИНИЯ, КАК ГОДОГРАФ РАДИУСА-ВЕКТОРА
Определение 1.2 Если начало всех векторов , помещено в начало координат, то они называются радиус–векторами.
Определение 1.3 Линия, являющаяся геометрическим местом концов радиусов-векторов , , называется годографом вектор-функции , а их общее начало – полюсом годографа.
Если параметр t – время, а — радиус-вектор движущейся точки, то годограф функции является траекторией движущейся точки.
Уравнение годографа можно записать в векторной форме (1.2) или в параметрическом виде:
(1.3)
В частности, если вектор-функция
с изменением аргумента меняет только свой модуль, а направление не изменяет (), то годографом такой вектор- функции будет прямолинейный луч, исходящий из начала координат; если же меняется только направление вектора, а модуль его остается неизменным (
), то годографом вектор-функции будет кривая, расположенная на сфере с центром в полюсе и радиусом, равным постоянному модулю вектора.
Рисунок 1.
1.3. ПРЕДЕЛ, НЕПРЕРЫВНОСТЬ И ПРОИЗВОДНАЯ ВЕКТОР–ФУНКЦИИ
Определение 1.
4 Вектор
называется пределом вектор-функции
при 
, если
.
(1.4)
Определение 1.5 Вектор-функция называется непрерывной в точке t 0, если она имеет в этой точке предел, равный значению вектор-функции в этой точке:
. (1.5)
Определение 1.6
Производной вектор-функции
в точке
t
называется предел отношения приращения вектор-функции к приращению аргумента 
при 
:
(1.6)
1.4. ГЕОМЕТРИЧЕСКИЙ И МЕХАНИЧЕСКИЙ СМЫСЛ ПЕРВОЙ ПРОИЗВОДНОЙ ВЕКТОР-ФУНКЦИИ
Геометрический смысл первой производной вектор-функции скалярного аргумента заключается в том, что эта производная представляет собой новый вектор, направленный по касательной к годографу:
. Покажем это.
Рисунок 2
Будем предполагать, что годограф рассматриваемой вектор-функции есть непрерывная линия, имеющая касательную в любой своей точке.
Дадим аргументу
t
приращение , тогда геометрически отношение 
— это некоторый вектор 
, лежащий на секущей ММ’. При этот вектор поворачивается и превращается в вектор 
, лежащий на касательной и направленный в сторону возрастания
t
.
Таким образом, вектор
(1.7)
будет единичным вектором касательной, ориентированный в сторону возрастания параметра t .
Следовательно, вектор
можно взять в качестве направляющего вектора касательной к кривой в точке ), (или 
), и уравнение касательной записать в виде:
(1.8)
Если
t
–
время, а
— радиус-вектор точки 
, движущейся в трёхмерном пространстве, то о
тношение называется средней скоростью точки на отрезке [
t
;
t
+
t
].
Механический смысл
первой производной вектор-функции заключается в том, что эта производная представляет собой скорость точки М в момент
t
: 
Правила дифференцирования вектор-функций
Докажем правило 1, пользуясь правилами вычитания векторов и деления вектора на число:
Доказательство остальных правил основываются на правиле 1 и правилах действий с векторами.
Пример 1.1 : Дана вектор-функция . Построить её годограф и составить уравнение ее касательной в произвольной точке.
Решение.
Для любой точки
(
x
,
y
,
z
)
годографа вектор – функции имеем:
x
=
acost
;
y
=
asint
;
z
=
bt
и поэтому при любом 
выполняется равенство
x
2
+
y
2
=
a
2
,
а образующая параллельна оси
Oz
.
Если параметр
t
интерпретировать как время, то при равномерном движении по окружности проекции конца радиус–вектора на плоскость
Oxy
его проекция на ось
Oz
будет двигаться равномерно и прямолинейно со скоростью
b
.
Иначе говоря, аппликата точки годографа вектор-функции растет пропорционально углу поворота ее проекции на плоскость
Oxy
. Поэтому искомый годограф будет иметь вид, изображенный на рис.3 и он называется винтовой линией. Для нахождения касательных к годографу (винтовой линии) найдем производную вектор–функции.
Решение. Поскольку , то и
Пример 2. Рассмотрим для примера функцию трех переменных f (х , у , z ), имеющую следующую таблицу истинности:
Матричный способ
Заключается в том, что множество переменных х n разбивается на две части у m и z n–m таким образом, что все возможные значения истинности вектора у m откладываются по строкам матрицы, а все возможные значения истинности вектора z n - m ― по столбцам. Значения истинности функции f на каждом наборе n = ( 1 , ..., m , m+ 1 ,..., n ) помещаются в клетки, образованные пересечением строки ( 1 , ..., m ) и столбца ( m+ 1 ,..., n ).
В рассмотренном выше Примере 2 в случае разбиения переменных (х, у, z ) на подмножества (х ) и (у, z ) матрица принимает вид:
|
у, z |
|||||
Существенной особенностью матричного способа задания является то, что полные наборы переменных х n , соответствующие соседним (как по вертикали, так и по горизонтали) клеткам, различаются по одной координате.
Задание с помощью полного бинарного дерева
Для описания n -местной функции f ( х n ) используется свойство бинарного дерева высоты n , заключающееся в том, что каждой висячей вершине в нем взаимно однозначно соответствует некоторый набор значений вектора х n . Соответственно, этой висячей вершине можно приписать такое же значение истинности, которое имеет на данном наборе функция f . В качестве примера (рис.1.3) приведем задание с помощью бинарного дерева рассмотренной выше трехместной функции f = (10110110).
Первый ряд цифр, приписанных висячим вершинам дерева, обозначает лексикографический номер набора, второй ― сам набор, а третий ― значение функции на нем.
Задание с помощью n - мерного единичного куба В n
Поскольку вершины В n также можно взаимно однозначно отобразить на множество всех наборов х n , то n -местную функцию f (х n ) можно задать, приписывая ее значения истинности соответствующим вершинам куба В n . На рис.1.4 показано задание функции f = (10110110) на кубе В 3 . Значения истинности приписаны вершинам куба.
Определение . Алгеброй логики называют множество булевых констант и переменных вместе с введенными на них логическими связками.
Формульное задание
Функции алгебры логики могут быть заданы в виде аналитических выражений.
Определение. Пусть Х ― алфавит переменных и констант, используемых в алгебре логики, F ― множество обозначений всех элементарных функций и их обобщений при числах переменных, превышающих 2.
Формулой над Х,F (формулой алгебры логики ) назовём все записи вида:
а) х, где х X ;
б) F 1 , F 1 &F 2 ,F 1 F 2 , F 1 F 2 , F 1 F 2 , F 1 F 2 , F 1 F 2 , F 1 F 2 , где F 1 , F 2 ― формулы над Х, F;
в) h (F 1 , … ,F n ), где n > 2, F 1 ,… , F n ― формулы над Х , F , h ― обозначение обобщенной пороговой функции из F .
Как следует из определения, для двухместных элементарных функций используется инфиксная форма записи, при которой функциональный символ помещают между аргументами, для отрицания и обобщенных функций используют префиксную форму записи, при которой функциональный символ ставят перед списком аргументов.
Пример 3.
1. Выражения х (у z ); (x , y , z u ) являются формулами алгебры логики, поскольку удовлетворяют данному выше определению.
2. Выражение х (у z ) не является формулой алгебры логики, поскольку неправильно применена операция .
Определение. Функцией, реализуемой формулой F , называется функция, получаемая при подстановке значений переменных в F . Обозначим ее f (F ).
Пример 4. Рассмотрим формулу F = ху (х z ). Для того, чтобы построить таблицу истинности реализуемой функции, необходимо последовательно с учетом силы логических связок выполнить логическое умножение ху , затем импликацию (х z ), после чего сложить полученные значения истинности по модулю 2. Результат выполнения действий показан в таблице:
|
х z | |||||
Формульное представление функций позволяет априори оценивать многие свойства функций. Переход от формульного задания к таблице истинности всегда может быть выполнен путем последовательных подстановок значений истинности в элементарные функции, входящие в формулу. Обратный переход неоднозначен, поскольку одна и та же функция может быть представлена различными формулами. Он требует отдельного рассмотрения.
и её дифференцирование.
Одним из наиболее простых способов задания пространственной кривой является задание векторного уравнения:
где
- радиус-вектор точки кривой, а
- параметр, определяющий положение
точки.
Т.о.
переменный вектор
есть функция скаляра
.
Такие функции в математическом анализе
называют векторными функциями скалярного
аргумента.
Разлагая
по ортам, уравнению (1) можно придать
вид:
Это разложение даёт возможность перейти к параметрическому уравнению кривой:
Другими словами, задание векторной функции равносильно заданию трёх скалярных.
По отношению к векторной функции (1), определяющему данную кривую, сама кривая называется годографом этой функции. Начало координат называют в этом случае полюсом годографа.
Пусть
теперь
и
- точки кривой, определяемой уравнением
(1). Причём
,
а
Радиус-векторы этих точек будут
и
.
Вектор
называют приращением векторной функции
,
соответствующее приращению
её аргумента, и обозначают через
,
Векторная
функция
будет непрерывной функцией
,
если
.
Для
нахождения производной от
поступим следующим образом –
.
Установим
теперь направление
.
Очевидно, что
коллинеарен с
и при
направлен в ту же сторону, что и
а при
- в противоположную сторону. Но в первом
случае
а во втором
Т.о. вектор
всегда направлен по секущей годографа
в сторону возрастания
.
Если
воспользоваться разложением
и
по ортам, то
Отсюда
деля (*) на
и переходя к пределу
для
получим
Опираясь на (4), можно показать, что справедливы следующие формулы:
(5) 
(6) 
- скалярная функция.
Доказательство (7).
Исследуем
теперь некоторые свойства
.
Прежде всего найдём его модуль:
.
Т.к.
мы считаем дугу годографа спрямляемой,
то тогда
- есть длина хорды, а
- длина дуги. Поэтому
Т.о. модуль производной от векторной функции скалярного аргумента равен производной от дуги годографа по тому же аргументу.
Следствие
1. Если
- единичный вектор, направленный по
касательной к годографу в сторону
увеличения
,
то
Следствие
2. Если за аргумент векторной функции
принята длина дуги годографа
,
то
(т.к.
)
Т.о. производная от векторной функции по длине дуги годографа равна единичному вектору касательной к годографу, направленному в сторону увеличения длины дуги.
Следствие
3. Если годограф векторной функции
рассматривать как траекторию движения
точки, а
- как время движения, отсчитываемое от
некоторого
,
то
по величине и направлению совпадает с
вектором скорости движения
.
В самом деле, скалярная величина скорости равна производной от пути по времени:
Кроме
того, вектор
направлен по касательной к траектории
в сторону движения, что соответствует
направлению возрастания
,
т.е. соответствует направлению
.
Т.о.
.
Рассмотрим
теперь
,
длина которого постоянна,
,
т.е.
(*) 
где
Дифференцируя (*), найдём:
Т.е.
В
частности, производный вектор от любого
переменного по направлению единичного
всегда
.
Пусть
теперь
угол между радиусами единичной сферы,
проведёнными в точки
и
годографа
.
Тогда длина хорды
из треугольника
будет равна
Модуль производной от единичного переменного вектора равен угловой скорости вращения этого вектора.
Как и для скалярных функций, дифференциал векторной функции записывается в виде
Но и тогда
Кривизна пространственной кривой.
Сопровождающий трёхгранник.
Согласно
следствию 2, для
можно записать формулу:
Изменение
направления
,
связанное с изменением касательной к
пространственной кривой, характеризует
кривизну кривой. За меру кривизны
пространственной кривой, как и для
плоской, принимают предел отношения
угла смежности к длине дуги, когда
кривизна,
угол
смежности,
длина
дуги.
С
другой стороны,
единичный
вектор и производный к нему вектор
перпендикулярен к нему, а его модуль
Дифференцируя
по
и
вводя
единичный
вектор с направлением
,
найдём:
Вектор
вектор
кривизны пространственной кривой. Его
направление, перпендикулярное к
направлению касательной, является
направлением нормали пространственной
кривой. Но пространственная кривая
имеет в любой точке бесчисленное
множество нормалей, которые все лежат
в плоскости,
проходящей
через данную точку кривой и перпендикулярно
к касательной в данной точке. Эту
плоскость называют нормальной плоскостью
пространственной кривой.
Определение.
Нормаль кривой, по которой направлен
вектор кривизны кривой в данной точке
– главная нормаль пространственной
кривой. Т.о.
единичный
вектор главной нормали.
Построим
теперь третий единичный вектор
равный векторному произведению
и
Вектор
,
как и
также перпендикулярен
т.е. лежит в нормальной плоскости. Его
направление называют направлением
бинормали пространственной кривой в
данной точке. Вектора
и
составляют тройку взаимно перпендикулярных
единичных векторов, направление которых
зависит от положения точки на
пространственной кривой и изменяется
от точки к точке. Эти вектора образуют
т.н. сопровождающий трехгранник
(трехгранник Френе) пространственной
кривой. Вектора
и
образуют правую тройку, так же как и
единичные орты
в правой системе координат.
Взятые
попарно
определяют три плоскости, проходящие
через одну и ту же точку на кривой и
образуют грани сопровождающего
трехгранника. При этом
и
определяют соприкасающую плоскость
(б.м. дуга кривой в окрестности данной
точки есть дуга плоской кривой в
соприкасаемой плоскости с точностью
до б.м. высшего порядка);
и
- спрямляющая плоскость;
и
- нормальная плоскость.
Уравнения касательной, нормали и бинормали.
Уравнения плоскостей сопровождающего трехгранника.
Зная
и
,
или любые коллинеарные им неединичные
вектораT,
N
и B
выведем уравнения, поименованные в этом
параграфе.
Для этого в каноническом уравнении прямой
и в уравнении плоскости, проходящей через данную точку
принять
за
координаты
выбранной на кривой точки, за
или соответственно за
принять координаты того из векторов
или
,
который определяет направление искомой
прямой или нормали к искомой плоскости:
или
- для касательной или нормальной
плоскости,
или
- для главной нормали и спрямляющей
плоскости,
или
- для бинормали и соприкасающейся
плоскости.
Если
кривая задана векторным уравнением
или
то за вектор
направленный
по касательной можно принять
Для
нахождения
и
найдём сначала разложение
по векторам
Ранее (следствие 1) мы нашли, что
Дифференцируя по
,
получим:
Но,
т.к.
Перемножим
теперь векторно
и
(*) 
На
основании (*) за вектор
,
имеющий направление бинормали, можнл
взять вектор
Но
тогда, за
можно принять векторное произведение
этих последних:
Т.о. в любой точке произвольной кривой мы можем определить все элементы сопроводдающего трехгранника.
Пример. Уравнение касательной, нормали и бинормали к правой винтовой линии в любой точке.
Касательная
Главнвя
нормаль
Бинормаль
Пусть множество значений вектор-функции скалярного аргумента приведено к общему началу в точке 0. Совместим с этой точкой начало декартовой системы координат. Тогда для любого вектор может быть разложен по ортам
Таким образом, задание вектор-функции скалярного аргумента означает задание трех скалярных функций 
При изменении значения аргумента конец вектора будет описывать в пространстве кривую, которая называется годографом вектора
Пусть для существует близкое значение 
Тогда производной вектор-функции поскалярному аргументу называется 
№17 Скорость и ускорение точки в криволинейном движении
Скорость
Скорость, вводится как характеристика движения материальной точки. Скорость является векторной величиной, которая характеризуется как быстротой движения (модуль вектора скорости), так и его направление (направление вектора скорости) в данный момент времени. Пусть материальная точка движется по какой-либо криволинейной траектории, при этом в момент времени t ей соответствует радиус-вектор r0 (рис. 1). За малый отрезок времени Δt точка совершит путь Δs и при этом получит элементарное (бесконечно малое) перемещение Δr.
Вектором средней скорости
Направление вектора средней скорости совпадает с направлением Δr. При бесконечном уменьшении Δt средняя скорость стремится к значению, которое называется мгновенной скоростью v:
Значит, мгновенная скорость v есть векторная величина, которая равна первой производной радиуса-вектора движущейся точки по времени. Т.к. в пределе секущая совпадает с касательной, то вектор скорости v направлен по касательной к траектории в сторону движения (рис. 2).
Рис.2
При уменьшении Δt, Δs все сильнее будет приближаться к |Δr|, поэтому модуль мгновенной скорости
Значит, модуль мгновенной скорости равен первой производной пути по времени:
При неравномерном движении модуль мгновенной скорости различен в разные моменты времени. В этом случае применяют скалярную величину
Если проинтегрировать по времени в пределах от t до t+Δt выражение ds=vdt (см. формулу (2)), то найдем длину пути, пройденного точкой за время Δt:
В случае равномерного движения числовое значение мгновенной скорости постоянно; Toгда выражение (3) примет вид
Длина пути, пройденного точкой за промежуток времени от t1 до t2, задается интегралом
УСКОРЕНИЕ
При неравномерном движения частно необходимо знать, как быстро изменяется скорость с течением времени. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, называется ускорение. Рассмотрим плоское движение - движение, при котором траектории каждой точки рассматриваемой системы лежат в одной плоскости. Пусть вектор v есть скорость точки А в момент времени t. За время Δt точка перешла в положение В и получила скорость, отличную от v как по модулю, так и направлению и равную v1+Δv. Перенесем вектор v1 в точку А и найдем Δv (рис. 1).
Средним ускорением неравномерного движения в интервале от t до t+Δt называется векторная величина, равная отношению изменения скорости Δv к интервалу времени Δt:
Мгновенным ускорением а (ускорением) материальной точки в момент времени t будет векторная величина:
равная первой производной скорости по времени.
Разложим вектор Δv на две составляющие. Для этого из точки А (рис. 1) по направлению скорости v отложим вектор AD, по модулю равный v1. Очевидно, что вектор CD, равный Δvτ, определяет изменение скорости за время Δt по модулю: Δvτ=v1-v. Вторая же составляющая Δvn вектора Δv характеризует изменение скорости за время Δt по направлению.
Тангенциальная составляющая ускорения:
т. е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.
Ищем вторую составляющую ускорения. Допускаем, что точка В сильно близка к точке А, поэтому Δs можно считать дугой окружности некоторого радиуса r, слабо отличающейся от хорды АВ. Треугольников АОВ подобен треугольнику EAD, из чего следует Δvn/AB=v1/r, но так как AB=vΔt, то
В пределе при Δt→0 получим v1→v.
Т.к. v1→v, угол EAD стремится к нулю, а т.к. треугольник EAD равнобедренный, то угол ADE между v и Δvn стремится к прямому. Следовательно, при Δt→0 векторы Δvn и v становятся взаимно перпендикулярными. Т.к. вектор скорости направлен по касательной к траектории, то вектор Δvn, перпендикулярный вектору скорости, направлен к центру кривизны траектории точки. Вторая составляющая ускорения, равная
называется нормальной составляющей ускорения и направлена по прямой перпендикулярной касательной к траектории (называемой нормалью) к центру ее кривизны (поэтому ее называют также центростремительным ускорением).
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис. 2):
Значит тангенциальная составляющая ускорения является характеристикой быстроты изменения скорости по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения - характеристикой быстроты изменения скорости по направлению (направлена к центру кривизны траектории). В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:
1)aτ=0, an=0 - прямолинейное равномерное движение;
2)aτ=an=const, аn=0 - прямолинейное равнопеременное движение. При таком виде движения
Если начальный момент времени t1 = 0, а начальная скорость v1 = v0, то, обозначив t2=t и v2 = v, получим a=(v-v0)/t, откуда
Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t найдем, что длина пути, пройденного точкой, в случае равнопеременного движения
3)aτ=f(t), an=0 - прямолинейное движение с переменным ускорением;
4)aτ=0, an=const. При aτ=0 скорость по модулю не изменяется, а изменяется по направлению. Из формулы an=v2/r следует, что радиус кривизны должен быть постоянным. Следовательно, движение по окружности является равномерным;равномерное криволинейное движение;
5)aτ=0, an≠0 равномерное криволинейное движение;
6)aτ=const, an≠0 - криволинейное равнопеременное движение;
7)aτ=f(t), an≠0 - криволинейное движение с переменным ускорением.
№18 Уравнения касательной плоскости и нормали к поверхности
Определение. Пусть на области D задана функция двух переменных z =f(х,у), M0(x0;y0) - внутренняя точка области D, M(x0+Δx;y+Δy) - "соседняя" с M0 точка из D.
Рассмотрим полное приращение функции:
Если Δz представлено в виде:
где A, B - постоянные (не зависящие от Δx, Δy), 
- расстояние между M и M0, α(Δ x,Δy) - бесконечно малая при Δx 0, Δy 0; тогда функция z =f(х,у) называется дифференцируемой в точке M0, а выражение
называется полным дифференциалом функции z =f(х;у) в точке M0.
Теорема 1.1. Если z =f(х;у) дифференцируема в точке M0, то
Доказательство
Так как в (1.16) Δx, Δy - произвольные бесконечно малые, то можно взять Δy =0, Δx≠0, Δx 0, тогда
после чего из (1.16) следует
Аналогично доказывается, что
и теорема 1.1. доказана.
Замечание: из дифференцируемости z =f(х,у) в точке M0 следует существование частных производных. Обратное утверждение неверно (из существования частных производных в точке M0 не следует дифференцируемость в точке M0).
В итоге, с учётом теоремы 1.1 формула (1.18) примет вид:
Следствие. Функция, дифференцируемая в точке M0, непрерывна в этой точке (так как из (1.17) следует, что при Δx 0, Δy 0: Δz 0, z(M) z(M0)).
Замечание: Аналогично для случая трех и более переменных. Выражение (1.17) примет вид:
Используя геометрический смысл (рис.1.3) частных производных и можно получить следующее уравнение (1.24) касательной плоскости πкасs к поверхности: z =f(х,у) в точке C0(x0,y0,z0), z0=z(M):
Из сравнения (1.24) и (1.21) получаем геометрический смысл полного дифференциала функции двух переменных:
Приращение аппликаты z при движении точки С по касательной плоскости из точки С0 в точку
где находится из (1.24).
Уравнение нормали Lн к поверхности: z =f(х,у) в точке С0 получается, как уравнение прямой, проходящей через С0 перпендикулярно к касательной плоскости:
№ 19 Производная по направлению. Градиент
Пусть в некоторой области задана функция 
и точка 
. Проведем из точки вектор , направляющие косинусы которого 
. На векторе , на расстоянии от его начала рассмотрим точку , т.е. .
Будем предполагать, что функция и ее частные производные первого порядка непрерывны в области.
Предел отношения при называется производной от функции в точке по направлению вектора и обозначается , т.е. .
Для нахождения производной от функции в заданной точке 
по направлению вектора 
используют формулу: ,
где – направляющие косинусы вектора , которые вычисляются по формулам: 
.
Пусть в каждой точке некоторой области задана функция .
Вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, называется градиентом функции и обозначается или (читается «набла у»): .
При этом говорят, что в области определено векторное поле градиентов.
Для нахождения градиента функции в заданной точке используют формулу: .
№22 основные свойства неопределенного интеграла
Неопределенный интеграл
где F - первообразная функции f (на промежутке); C - произвольная постоянная.
Основные свойства
1. 
2. 
3. Если 
то
24) 
25) 
28) 
Этот метод применяется в тех случаях, когда подынтегральное выражение представляет собой произведение или частное разнородных ф-ций. При этом за V’(x) принимается та часть, которая легко интегрируется.
29) 
32) Разложение рациональной дроби на простейшие дроби .
Всякую правильную рациональную дробь 
можно представить в виде суммы конечного числа простейших рациональных дробей первого – четвертого типов. Для разложения на простейшие дроби необходимо разложить знаменатель Q m (x)
на линейные и квадратные множители, для чего надо решить уравнение:
- (5)
Теорема.
Правильную рациональную дробь
, где
, можно единственным образом разложить на сумму простейших дробей:
- (6)
(A 1 , A 2 , …, A k , B 1 , B 2 , …, B 1 , M 1 , N 1 , M 2 , M 2 , …, M s , N s – некоторые действительные числа).
33) Разложение правильной дроби на простейшие дроби при комплексных корнях знаменателя
Постановка задачи. Найти неопределенный интеграл
1 . Введем обозначения:
Сравним степени числителя и знаменателя.
Если подынтегральная функция – неправильная рациональная дробь, т.е. степень числителя n больше или равна степени знаменателя m , то сначала выделяем целую часть рациональной функции, поделив числитель на знаменатель:
Здесь многочлен – остаток от деления на причем степень Pk(x) меньше степени Qm
2 . Разложим правильную рациональную дробь
на элементарные дроби.
Если ее знаменатель имеет простые комплексные корни т.е.
то разложение имеет вид
3 . Для вычисления неопределенных коэффициентов, A1,A2,A3...B1,B1,B3... приводим к общему знаменателю дроби в правой части тождества, после чего приравниваем коэффициенты при одинаковых степенях X в числителях слева и справа. Получим систему 2 S уравнений с 2 S неизвестными, которая имеет единственное решение.
4 Интегрируем элементарные дроби вида
47) Если существует конечный предел I интегральной суммы при λ → 0, и он не зависит от способа выбора точек ξ i, способа разбиения отрезка, то этот предел называется определенным интегралом от функции f (x)по отрезку и обозначается следующим образом:
В этом случае функция f (x) называется интегрируемой на . Числа a и b называются соответственно нижним и верхним пределами интегрирования, f (x) – подынтегральной функцией, х – переменной интегрирования. Следует заметить, что не имеет значения, какой буквой обозначена переменная интегрирования определенного интеграла
поскольку смена обозначений такого рода никак не влияет на поведение интегральной суммы. Несмотря на сходство в обозначениях и терминологии, определенный и неопределенный интегралы различны
48) Теорема о существовании определённого интеграла
Разобьем отрезок на части точками x1,x2,x3... так что
Обозначим через deltaX длину i-го кусочка и через максимальную из этих длин.
Выберем на каждом отрезке произвольным образом некоторую точку так что (она называется «средней точкой»), и составим
величину, которая называется интегральной суммой
Найдем теперь предел
Определение. Если существует и он не зависит от
а) способа разбиения отрезка на части и от
б) способа выбора средней точки,
есть определенный интеграл от функции f(x) по отрезку .
Функция f(x) называется в этом случае интегрируемой на отрезке . Величины a и b называются нижним и верхним пределами интегрирования соответственно.
50) Основные св-ва определённого интегрирала
1)Если промежуток интегрирования разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке , равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
2)теорема о среднем значении.
Пусть функция y = f(x) интегрируема на отрезке ,m=min f(x) и M=max f(x) , тогда существует такое число
Следствие.
Если функция y = f(x) непрерывна на отрезке , то найдется такое число, что.
3)При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
4)Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
5)Интегрирование модуля функции
Если функция f(x) интегрируема,то и её модуль интегрируем на отрезке.
6)Интегрирование неравенства
Если f(x) и q(x) интегрируемы на отрезке и х принадлежит
то
7)Линейность
Постоянный множитель можно выносить за знак определенного интеграла
если f(x) существует и интегрируема на отрезке , A=const
Если функция y=f(x) непрерывна на отрезке и F(x) – какая-либо ее первообразная на (F’(x)=f(x)), то имеет место формула
Пусть для вычисления интеграла от непрерывной функции сделана подстановка x=α(t).
1) Функция x=α(t) и ее производная x’=α’(t) непрерывны при t принадлежащей
2) Множеством значений функции x=α(t) при t принадлежащей является отрезок
3) A α(c)=a и α(v)=b
Пусть функция f(x) непрерывна на промежутке и имеет бесконечный разрыв при x=b. Если существует предел , то его называют несобственным интегралом второго рода и обозначают .
Таким образом, по определению,
Если предел в правой части существует, то несобственный интеграл сходится. Если же указанный предел не существует или бесконечен, то говорят, что интеграл расходится.
