Синтаксический анализ. Принцип рекурсии в правилах грамматики Алгоритм удаления левой рекурсии реализация

Основная трудность при использовании предсказывающего анализа - это нахождение такой грамматики для входного языка, по которой можно построить таблицу анализа с однозначно определенными входами. Иногда с помощью некоторых простых преобразований грамматику, не являющуюся LL(1), можно привести к эквивалентной LL(1)-грамматике. Среди этих преобразований наиболее эффективными являются левая факторизация и удаление левой рекурсии . Здесь необходимо сделать два замечания. Во-первых, не всякая грамматика после этих преобразований становится LL(1), и, во-вторых, после таких преобразований получающаяся грамматика может стать менее понимаемой.

Непосредственную левую рекурсию, то есть рекурсию вида , можно удалить следующим способом. Сначала группируем A -правила:

где никакая из строк не начинается с A. Затем заменяем этот набор правил на

где A" - новый нетерминал. Из нетерминала A можно вывести те же цепочки, что и раньше, но теперь нет левой рекурсии . С помощью этой процедуры удаляются все непосредственные левые рекурсии , но не удаляется левая рекурсия, включающая два или более шага. Приведенный ниже алгоритм 4.8 позволяет удалить все левые рекурсии из грамматики.

Алгоритм 4.8 . Удаление левой рекурсии .

Вход . КС-грамматика G без e-правил (вида A -> e).

Выход . КС-грамматика G" без левой рекурсии , эквивалентная G.

Метод . Выполнить шаги 1 и 2.

(1) Упорядочить нетерминалы грамматики G в произвольном порядке.

(2) Выполнить следующую процедуру:

После (i-1) -й итерации внешнего цикла на шаге 2 для любого правила вида , где k < i, выполняется s > k. В результате на следующей итерации (по i) внутренний цикл (по j) последовательно увеличивает нижнюю границу по m в любом правиле , пока не будет m >= i. Затем, после удаления непосредственной левой рекурсии для A i -правил, m становится больше i.

Алгоритм 4.8 применим, если грамматика не имеет e - правил (правил вида A -> e). Имеющиеся в грамматике e - правила могут быть удалены предварительно. Получающаяся грамматика без левой рекурсии может иметь e -правила.

Левая факторизация

Oсновная идея левой факторизации в том, что в том случае, когда неясно, какую из двух альтернатив надо использовать для развертки нетерминала A, нужно изменить A -правила так, чтобы отложить решение до тех пор, пока не будет достаточно информации для принятия правильного решения.

Если - два A -правила и входная цепочка начинается с непустой строки, выводимой из мы не знаем, разворачивать ли по первому правилу или по второму. Можно отложить решение, развернув . Тогда после анализа того, что выводимо из можно развернуть по или по . Левофакторизованные правила принимают вид

Алгоритм 4.9 . Левая факторизация грамматики.

Вход . КС-грамматика G.

Выход . Левофакторизованная КС-грамматика G", эквивалентная G.

Метод . Для каждого нетерминала A найти самый длинный префикс общий для двух или более его альтернатив. Если , то есть существует нетривиальный общий префикс, заменить все A -правила

где z обозначает все альтернативы, не начинающиеся с на

где A" - новый нетерминал. Применять это преобразование, пока никакие две альтернативы не будут иметь общего префикса.

Пример 4.9 . Рассмотрим вновь грамматику условных операторов из примера 4.6 :

S -> if E then S | if E then S else S | a E -> b

После левой факторизации грамматика принимает вид

S -> if E then SS" | a S" -> else S | e E -> b

К сожалению, грамматика остается неоднозначной, а значит, и не LL(1)-грамматикой.

При процедуре рекурсивного разбора сверху вниз может возникнуть проблема бесконечного цикла.

В грамматике для арифметических операций применение второго правила приведет к зацикливанию процедуры разбора. Подобные грамматики называются леворекурсивными. Грамматика называется леворекурсивной, если в ней существует нетерминал А, для которого существует вывод А=>+Аa. В простых случаях левая рекурсия вызвана правилами вида

В этом случае вводят новый нетерминал и исходные правила заменяют следующими.

(если есть нетерминал А, для которого существует вывод А→+Аa за 1 или более шагов). Левой рекурсии можно избежать, преобразовав грамматику.

Например, продукции A→Aa

Можно заменить на эквивалентные:

Для такого случая существует алгоритм, исключающий левую рекурсию:

1) определяем на множестве нетерминалов какой-либо порядок (А 1 , А 2 , …, А n)

2) берем каждый нетерминал, если для него есть продукция, учитывающая нетерминал, стоящий левее, и преобразуем грамматику:

for i:=1 to n do

for j:=1 to i-1 do

if Ai → Ajγ then Ai→δ1γ

│ δkγ, где

Aj → δ1│ δ2│ …│ δk

3) исключаем все случаи непосредственной левой рекурсии (правило1)

Т.о. алгоритм помогает избежать зацикливания.

Исключение левой рекурсии из грамматики арифметических выражений и общий вид правила исключения левой рекурсии:

Общий вид правила исключения левой рекурсии

Левая факторизация.

LL(1)-грамматики нужны для того, чтобы выбрать нужную продукцию для разбора сверху-вниз, чтобы не произошло зацикливание.

Иногда существует возможность преобразовать грамматику к LL(1) виду, используя метод левой факторизации.

Например: S→ if B then S

│if B then S else S

Эти продукции нарушают условие LL(1)-грамматик. Эту грамматику можно преобразовать к виду LL(1).

S → if B then S Tail

В общем виде это преобразование можно определить так:

вводим новый нетерминал В, для которого

| β N Для B можно применить левую факторизацию. Эта процедура повторяется, пока остается неопределенным выбор продукции (т.е. пока в ней можно что-нибудь изменить).

Построение множества FIRST

Множество First для нетерминала определяет множество терминалов, с которых может начинаться данный нетерминал.

1. Если х - терминал, то first(x)={x}. Так как первым символом последовательности из одного терминала может являться только сам терминал.

2. Если в грамматике присутствует правило Хà e, то множество first(х) включает e. Это означает, что Х может начинаться с пустой последовательности, то есть отсутствовать вообще.

3. Для всех продукций вида XàY1 Y2 … Yk выполняем следующее. Добавляем в множество first(Х) множество first(Yi) до тех пор, пока first(Yi-1) содержит e, а first(Yi) не содержит e. При этом i изменяется от 0 до k. Это необходимо, так как если Yi-1 может отсутствовать, то необходимо выяснить, с чего будет начинаться вся последовательность в этом случае.

Определение 10.1 Некоторый нетерминальный символ А контекстно-свободной грамматики G = (N, P, S) называется рекурсивным, если существует вывод А + А для некоторых и. Если при этом =, то А называется леворекурсивным. Аналогично, если =, то А называется праворекурсивным. Грамматика, имеющая хотя бы один леворекурсивный нетерминальный символ, называется леворекурсивной. Грамматика, в которой все нетерминальные символы, кроме, быть может, начального символа, рекурсивные, называется рекурсивной.

Заметим, что для рекурсивных грамматик в выводе А + А всегда либо, либо. Если = и =, то грамматика G является циклической грамматикой. Пример Примером праворекурсивной грамматики является грамматика со следующей схемой: 1 0 Данная грамматика порождает множество чисел, состоящих из нулей и единиц.

Пример Тот же самый язык, что и в примере порождает леворекурсивная грамматика со следующей схемой: 1 0

Пример Примером леворекурсивной грамматики является грамматика со следующей схемой: А 1 0 Данная грамматика порождает множество идентификаторов, начинающихся с буквы А.

Пример Тот же самый язык, что и в примере порождает праворекурсивная грамматика со следующей схемой: А 1 0

Лемма 10.1 Пусть G = (N, P, S) – КС-грамматика, в которой для некоторого нетерминального символа А все А- правила имеют вид А A 1 | A 2 | … | A m | 1 | 2 | … | n | причем ни одна из цепочек i не начинается с А. Пусть G"=(N {A"}, P", S), где A" – новый нетерминал, а P" получается из P заменой этих А- правил следующими правилами А 1 | 2 | … | n | 1A" | 2A" | … | nA" | А" 1 | 2 | … | m | 1A" | 2A" | … | mA" Тогда L(G") = L(G). Рассмотрим алгоритм преобразования КС- грамматики, в которой имеется непосредственная левая рекурсия, к КС-грамматике без левой рекурсии.

Доказательство. Цепочки, которые можно получить в грамматике G из нетерминала А применением А- правил лишь к самому левому нетерминалу, образуют регулярное множество (… + n)(… + m)* Это в точности те цепочки, которые можно получить в грамматике G" из А с помощью правых выводов, применив один раз А-правило и несколько раз А"- правила (в результате вывод уже не будет левым). Все шаги вывода, на которых не используются А- правила, можно непосредственно сделать и в грамматике G", так как не А-правила в обеих грамматиках одни и те же. Отсюда можно заключить, что L(G) L(G").

Обратное включение доказывается аналогично. В грамматике G" берется правый вывод и рассматриваются последовательности шагов, состоящие из одного применения А-правила и нескольких применений А"-правил. Таким образом, L(G") = L(G). Грамматика примера получена из грамматики примера с использованием преобразования леммы 10.1.

Лемма 10.2 Пусть G = (N, P, S) – КС-грамматика, в которой для некоторого нетерминального символа А все А- правила имеют вид А A 1 | A 2 | … | A m | 1 | 2 | … | m причем ни одна из цепочек i не начинается с А. Пусть G"=(N, P", S), где P" получается из P заменой этих А-правил следующими правилами А 1 | 2 | … | m | 1A | 2A | … | mA Тогда L(G") = L(G). Грамматика примера получена из грамматики примера с использованием преобразования леммы 10.2.

На рисунке показано, как действуют преобразования на дерево вывода A A i1... i2 A A ik A ik A ik-1... i1

Пример Пусть G0 – обычная грамматика с правилами E E+T E T T T*F T F F (E) F a Эквивалентная ей грамматика G`

E T E TE" E" +T E" +TE" T F T FT " T " *F T " *FT " F (E) F a Рассмотрим теперь, как преобразовать приведенную леворекурсивную КС-грамматику к КС-грамматике, не имеющей левой рекурсии.

Алгоритм 10.2 Устранение левой рекурсии. Вход: Приведенная КС-грамматика G=(N,P,S) Выход: Эквивалентная КС-грамматика G` без левой рекурсии. Метод. Пусть N = {A1,…, An}, т.е. все нетерминальные символы грамматики упорядочены некоторым произвольным образом. Преобразуем G так, чтобы в правиле Ai цепочка начиналась либо с терминала, либо с такого Aj, что j i. 1) Положим i=1.

2) Пусть множество Ai – правил – это Ai Ai | … | Ai m | 1 | … | p, где ни одна из цепочек j не начинается с Ak, если k i (если это не выполнено, можно ввести новый нетерминальный символ, заменить первый символ правила этим символом и добавить дополнительное правило в грамматику). Заменим Ai–правила правилами: Ai 1 | … | p | 1Ai" | … | pAi" Ai" 1 | … | m | 1Ai" | … | mAi" где A"i новый нетерминал. Правые части всех Ai- правил начинаются теперь с терминала или с Ak для некоторого k > i. 3) Если i=n, полученную грамматику G" считать результатом и остановиться. В противном случае положить i=i+1 и j=1. i. 3) Если i=n, полученную грамматику G" считать результатом и остановиться. В противном случае положить i=i+1 и j=1.">

J, то и правая часть каж" title="4) Заменить каждое правило вида Ai Aj правилами Ai 1 |…| m, полученными в результате замены Aj правыми частями всех Aj-правил вида Aj 1|…| m. Так как правая часть каждого Aj-правила начинается уже с терминала или с Ak для k > j, то и правая часть каж" class="link_thumb"> 16 4) Заменить каждое правило вида Ai Aj правилами Ai 1 |…| m, полученными в результате замены Aj правыми частями всех Aj-правил вида Aj 1|…| m. Так как правая часть каждого Aj-правила начинается уже с терминала или с Ak для k > j, то и правая часть каждого Ai- правила будет теперь обладать этим свойством. 5) Если j=i–1, перейти к шагу (2). В противном случае положить j=j+1 и перейти к шагу (4). j, то и правая часть каж"> j, то и правая часть каждого Ai- правила будет теперь обладать этим свойством. 5) Если j=i–1, перейти к шагу (2). В противном случае положить j=j+1 и перейти к шагу (4)."> j, то и правая часть каж" title="4) Заменить каждое правило вида Ai Aj правилами Ai 1 |…| m, полученными в результате замены Aj правыми частями всех Aj-правил вида Aj 1|…| m. Так как правая часть каждого Aj-правила начинается уже с терминала или с Ak для k > j, то и правая часть каж"> title="4) Заменить каждое правило вида Ai Aj правилами Ai 1 |…| m, полученными в результате замены Aj правыми частями всех Aj-правил вида Aj 1|…| m. Так как правая часть каждого Aj-правила начинается уже с терминала или с Ak для k > j, то и правая часть каж">

Теорема 10.1 Для каждого КС-языка существует порождающая его не леворекурсивная грамматика. Доказательство есть следствие приведенных в данном разделе преобразований. Пример Пусть G есть КС-грамматика с правилами A BC a B CA Ab C AB CC a

Положим A1=A, A2=B и A3=C После каждого применения шага (2) или (4) алгоритма получаются следующие грамматики (указываем только новые правила). Шаг (2) для i=1: G не меняется Шаг (4) для i=2, j=1: B CA BCb ab Шаг (2) для i=2: B CA ab CAB abB B Cb Шаг (4) для i=3, j=1: C BCB aB CC a Шаг (4) для i=3, j=2: C CACB ab CB CAB CB ab B CB aB CC a Шаг (2) для i=3: C abCB ab B CB aB a abCBC ab B CB C aB C aC C ACB C AB CB C CC ACB AB CB C

LL (k)- грамматикой, если для данной цепочки и первых k символов (если они есть), выводящихся из , существует не более одного правила, которое можно применить к A , чтобы получить вывод какой-нибудь терминальной цепочки,

Рис. 4.4.

начинающейся с и продолжающейся упомянутыми k терминалами.

Грамматика называется LL (k)-грамматикой, если она LL (k)- грамматика для некоторого k .

Пример 4.7 . Рассмотрим грамматику G = ({S, A, B}, {0, 1, a, b}, P, S) , где P состоит из правил

S -> A | B, A -> aAb | 0, B -> aBbb | 1.

Здесь . G не является LL (k)-грамматикой ни для какого k. Интуитивно, если мы начинаем с чтения достаточно длинной цепочки, состоящей из символов a , то не знаем, какое из правил S -> A и S -> B было применено первым, пока не встретим 0 или 1 .

Обращаясь к точному определению LL (k)-грамматики, положим и y = a k 1b 2k . Тогда выводы

соответствуют выводам (1) и (2) определения. Первые k символов цепочек x и y совпадают. Однако заключение ложно. Так как k здесь выбрано произвольно, то G не является LL -грамматикой.

Следствия определения LL(k)- грамматики

Теорема 4.6 . КС-грамматика является LL(k)-грамматикой тогда и только тогда, когда для двух различных правил и из Р пересечение пусто при всех таких , что .

Доказательство . Необходимость . Допустим, что и удовлетворяют условиям теоремы, а содержит x . Тогда по определению FIRST для некоторых y и z найдутся выводы

(Заметим, что здесь мы использовали тот факт, что N не содержит бесполезных нетерминалов, как это предполагается для всех рассматриваемых грамматик.) Если |x| < k ; то y = z = e . Так как , то G не LL (k)- грамматика .

Достаточность . Допустим, что G не LL (k)- грамматика .

Тогда найдутся такие два вывода

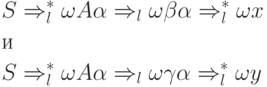
что цепочки x и y совпадают в первых k позициях, но . Поэтому и - различные правила из P и каждое из множеств и содержит цепочку FIRST k (x) , совпадающую с цепочкой FIRST k (y) .

Пример 4.8 . Грамматика G , состоящая из двух правил S -> aS | a , не будет LL (1)-грамматикой, так как

FIRST 1 (aS) = FIRST 1 (a) = a .

Интуитивно это можно объяснить так: видя при разборе цепочки, начинающейся символом a , только этот первый символ, мы не знаем, какое из правил S -> aS или S -> a надо применить к S . С другой стороны, G - это LL (2)- грамматика . В самом деле, в обозначениях только что представленной теоремы, если , то A = S и . Так как для S даны только два указанных правила, то и . Поскольку FIRST2(aS) = aa и FIRST2(a) = a , то по последней теореме G будет LL (2)-грамматикой.

Удаление левой рекурсии

Основная трудность при использовании предсказывающего анализа - это нахождение такой грамматики для входного языка, по которой можно построить таблицу анализа с однозначно определенными входами. Иногда с помощью некоторых простых преобразований грамматику, не являющуюся LL(1), можно привести к эквивалентной LL(1)-грамматике. Среди этих преобразований наиболее эффективными являются левая факторизация и удаление левой рекурсии . Здесь необходимо сделать два замечания. Во-первых, не всякая грамматика после этих преобразований становится LL(1), и, во-вторых, после таких преобразований получающаяся грамматика может стать менее понимаемой.

Непосредственную левую рекурсию, то есть рекурсию вида , можно удалить следующим способом. Сначала группируем A -правила:

где никакая из строк не начинается с A . Затем заменяем этот набор правил на

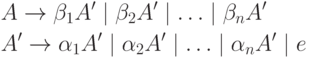
где A" - новый нетерминал. Из нетерминала A можно вывести те же цепочки, что и раньше, но теперь нет левой рекурсии . С помощью этой процедуры удаляются все непосредственные левые рекурсии , но не удаляется левая рекурсия, включающая два или более шага. Приведенный ниже алгоритм 4.8 позволяет удалить все левые рекурсии из грамматики.

Алгоритм 4.8 . Удаление левой рекурсии .

Вход . КС-грамматика G без e-правил (вида A -> e ).

Выход . КС-грамматика G" без левой рекурсии , эквивалентная G .

Метод . Выполнить шаги 1 и 2.

(1) Упорядочить нетерминалы грамматики G в произвольном порядке.

(2) Выполнить следующую процедуру:

После (i-1) -й итерации внешнего цикла на шаге 2 для любого правила вида , где k < i , выполняется s > k . В результате на следующей итерации (по i ) внутренний цикл (по j ) последовательно увеличивает нижнюю границу по m в любом правиле , пока не будет m >= i . Затем, после удаления непосредственной левой рекурсии для A i -правил, m становится больше i .