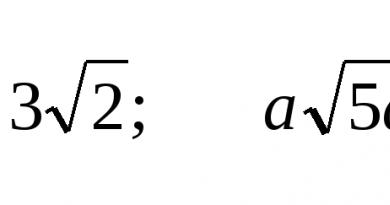Omkrets er samlingen av alle punkter i planet like langt fra ett gitt punkt, kalt midten av sirkelen. Avstanden fra sentrum av sirkelen til et hvilket som helst punkt på sirkelen kalles . radius av sirkelen.

- kanonisk ligning av en sirkel (16) - sentrum av sirkelen.

Hvis sentrum av sirkelen ligger ved origo, så er ligningen for sirkelen (16 .)

Ellipse er samlingen av alle punkter i planet, summen av avstandene fra to gitte punkter i dette planet (kalt triks av denne ellipsen) er en konstant verdi.

I (0;b)M(x,y)

r 1 r 2 r 1 + r 2 = 2a

(-a;0) F 1 (-c; 0) 0 F 2 (c; 0) (a; 0) X

La oss for korthets skyld betegne a 2 -b 2 =c 2 (*), så er ellipsens ligning: (17)

Hvis du setter y=0, får du , og hvis du setter x=0, får du ; dette betyr at og er lengdene til halvaksene til ellipsen – stor() Og liten(). I tillegg kan ikke hver av begrepene på venstre side være større enn én, derfor , , og derfor er hele ellipsen plassert inne i rektangelet. Punktene A,B,C,D, der ellipsen skjærer dens symmetriakser kalles toppene av ellipsen.

Holdning kalles ellipsens eksentrisitet.

Hyperbole er settet av alle punkter i planet, modulen til forskjellen i avstander fra to gitte punkter i dette planet (kalt triks av denne hyperbelen) er en konstant verdi. Midtpunktet på avstanden mellom brennpunktene kalles sentrum av hyperbelen.

r 2 r 1 – r 2 = 2a

F 1 (-c; 0) 0 F 2 (c; 0) x

La oss betegne a 2 -c 2 = -b 2 (**), hyperbelligningen: (18)

Fra denne ligningen er det klart at en hyperbel har to symmetriakser (hovedakser), samt et symmetrisenter (sentrum av hyperbelen).

Holdning kalles eksentrisiteten til hyperbelen.

Hvis du setter y=0, får du , og hvis du setter x=0, får du .

Dette betyr at okseaksen skjærer hyperbelen på to punkter (hjørnepunktene til hyperbelen), dette er - ekte akse; Oy-aksen skjærer ikke hyperbelen - dette er " imaginær akse. "Ethvert segment som forbinder to punkter i en hyperbel, hvis det passerer gjennom sentrum, kalles diameteren til hyperbelen.

En rett linje som en buet linje nærmer seg så nært som ønsket, men aldri krysser den kalles asymptote av kurven. En hyperbel har to asymptoter. Deres ligninger er: (19)

Parabel er samlingen av alle punkter på planet, avstanden fra hvert av disse til et gitt punkt (kalt fokus) lik avstanden til en gitt rett linje (kalt rektor).

- parabel parameter.

En parabel har én symmetriakse. Skjæringspunktet for en parabel med symmetriaksen kalles toppunktet til parablen.

Den kanoniske ligningen til en parabel med et toppunkt ved opprinnelsen, hvis symmetriakse er okseaksen og grener rettet mot høyre har formen (20)

Rektorens ligning:

Den kanoniske ligningen til en parabel med et toppunkt ved opprinnelsen, hvis symmetriakse er okseaksen og grener rettet mot venstre har formen (20 ,)

Rektorens ligning:

Den kanoniske ligningen til en parabel med et toppunkt ved opprinnelsen, hvis symmetriakse er Oy-aksen og grener rettet oppover har formen (20 ,)

Rektorens ligning:

Den kanoniske ligningen til en parabel med et toppunkt ved origo, hvis symmetriakse er Oy-aksen og grener rettet nedover har formen (20 ,)

Rektorens ligning:

y y

F 0 p/2 x -p/2 0 x

Å å

s/2

–p/2
Tema 2.1. Forelesning 7. Leksjon 10

Emne: Funksjoner av en uavhengig variabel, deres grafer.

Begrepet funksjon

Et av de grunnleggende matematiske begrepene er funksjonsbegrepet. Konseptet med en funksjon er assosiert med å etablere en avhengighet (forbindelse) mellom elementene i to sett.

La to ikke-tomme sett X og Y gis. Korrespondansen ƒ, som tilsvarer hvert element xО X ett og bare ett element уО Y, kalles en funksjon og skrives y=ƒ(x), xО X eller ƒ. : X→Y. De sier også at funksjonen ƒ kartlegger mengden X til mengden Y.

For eksempel er samsvarene ƒ og g vist i figur 98 a og b funksjoner, men de i figur 98 c og d er det ikke. I tilfelle i - svarer ikke hvert element xÎX til et element yÎY. I tilfelle d er unikhetsvilkåret ikke oppfylt.

Mengden X kalles definisjonsdomenet til funksjonen ƒ og er betegnet med D(f). Settet med alle уОY kalles settet med verdier til funksjonen ƒ og er betegnet E(ƒ).

Numeriske funksjoner. Funksjonsgraf. Metoder for å spesifisere funksjoner

La en funksjon ƒ : X→Y gis.

Hvis elementene i mengdene X og Y er reelle tall (dvs. XÌ R og YÌ R), kalles funksjonen ƒ en tallfunksjon. I fremtiden vil vi studere (som regel) numeriske funksjoner, for korthets skyld vil vi ganske enkelt kalle dem funksjoner og skrive y=ƒ(x).

Variabelen x kalles et argument eller uavhengig variabel, og y kalles en funksjon eller avhengig variabel (av x). Når det gjelder selve mengdene x og y, sies de å være funksjonelt avhengige. Noen ganger skrives den funksjonelle avhengigheten til y av x på formen y = y (x), uten å introdusere en ny bokstav (ƒ) for å indikere avhengigheten.

Privat verdi funksjoner ƒ(x) for x=a skrives som følger: ƒ(a). For eksempel, hvis ƒ(x)=2x 2 -3, så ƒ(0)=-3, ƒ(2)=5.

Funksjonsgraf y=(x) er settet av alle punkter i Oxy-planet, for hver av dem er x verdien av argumentet, og y er den tilsvarende verdien av funksjonen.

For eksempel er grafen til funksjonen y=√(1-2) den øvre halvsirkelen med radius R=1 med sentrum ved O(0;0) (se fig. 99).

For å sette funksjonen y=ƒ(x), er det nødvendig å spesifisere en regel som tillater, å vite x, å finne den tilsvarende verdien av y.

De vanligste tre måtene å spesifisere en funksjon på er: analytisk, tabellform og grafisk.

Analytisk metode: En funksjon er spesifisert som én eller flere formler eller ligninger.

Hvis definisjonsdomenet til funksjonen y = ƒ(x) ikke er spesifisert, antas det at det faller sammen med settet med alle verdiene til argumentet som den tilsvarende formelen gir mening for. Dermed er definisjonsdomenet til funksjonen y = √(1-x2) segmentet [-1; 1].

Den analytiske metoden for å spesifisere en funksjon er den mest avanserte, siden den inkluderer metoder for matematisk analyse som gjør det mulig å fullt ut studere funksjonen y=ƒ(x).

Grafisk metode: grafen til funksjonen er spesifisert.

Ofte tegnes grafer automatisk ved å ta opp instrumenter eller vises på en skjerm. Verdiene til funksjonen y som tilsvarer visse verdier av argumentet x er direkte funnet fra denne grafen.

Fordelen med en grafisk oppgave er dens klarhet, ulempen er unøyaktigheten.

Tabellmetode: en funksjon spesifiseres av en tabell med en serie argumentverdier og tilsvarende funksjonsverdier. For eksempel de velkjente verditabellene trigonometriske funksjoner, logaritmiske tabeller.

I praksis er det ofte nødvendig å bruke tabeller med funksjonsverdier oppnådd eksperimentelt eller som et resultat av observasjoner.

Andre ordens kurver på et plan er linjer definert av ligninger der variabelen koordinerer x Og y er inneholdt i andre grad. Disse inkluderer ellipsen, hyperbelen og parabelen.

Den generelle formen for den andre ordenskurveligningen er som følger:

Hvor A, B, C, D, E, F- tall og minst én av koeffisientene A, B, C ikke lik null.

Når man løser problemer med andreordenskurver, vurderes oftest de kanoniske ligningene til ellipsen, hyperbelen og parabelen. Det er lett å gå videre til dem fra generelle ligninger; eksempel 1 på problemer med ellipser vil bli viet til dette.

Ellipse gitt av den kanoniske ligningen

Definisjon av en ellipse. En ellipse er settet av alle punkter i planet der summen av avstandene til punktene kalt foci er en konstant verdi større enn avstanden mellom fociene.

Fokusene er angitt som i figuren nedenfor.

Den kanoniske ligningen til en ellipse har formen:

Hvor en Og b (en > b) - lengdene til halvaksene, dvs. halvparten av lengdene til segmentene avskåret av ellipsen på koordinataksene.

Den rette linjen som går gjennom brennpunktene til ellipsen er dens symmetriakse. En annen symmetriakse til en ellipse er en rett linje som går gjennom midten av et segment vinkelrett på dette segmentet. Prikk OM skjæringspunktet mellom disse linjene fungerer som senter for symmetri av ellipsen eller rett og slett senter av ellipsen.

Abscisseaksen til ellipsen skjærer i punktene ( en, OM) Og (- en, OM), og ordinataksen er i punkter ( b, OM) Og (- b, OM). Disse fire punktene kalles ellipsens toppunkter. Segmentet mellom hjørnene av ellipsen på x-aksen kalles dens hovedakse, og på ordinataksen - dens mindre akse. Segmentene deres fra toppen til midten av ellipsen kalles halvakser.

Hvis en = b, så tar ellipsens ligning formen . Dette er ligningen til en sirkel med radius en, og en sirkel er et spesialtilfelle av en ellipse. En ellipse kan fås fra en sirkel med radius en, hvis du komprimerer den til en/b ganger langs aksen Oy .

Eksempel 1. Sjekk om en linje gitt av en generell ligning er , ellipse.

Løsning. Vi transformerer den generelle ligningen. Vi bruker overføringen av den frie termen til høyre side, term-for-term-deling av ligningen med samme tall og reduksjon av brøker:

Svare. Ligningen oppnådd som et resultat av transformasjonene er den kanoniske ligningen for ellipsen. Derfor, denne linjen- ellipse.

Eksempel 2. Komponer den kanoniske ligningen til en ellipse hvis halvaksene er lik henholdsvis 5 og 4.

Løsning. Vi ser på formelen for den kanoniske ligningen for en ellipse og erstatning: halvhovedaksen er en= 5, er semiminoraksen b= 4. Vi får den kanoniske ligningen til ellipsen:

Punkter og , angitt i grønt på hovedaksen, hvor

kalles triks.

ringte eksentrisitet ellipse.

Holdning b/en karakteriserer "oblateness" av ellipsen. Jo mindre dette forholdet er, jo mer er ellipsen forlenget langs hovedaksen. Imidlertid er graden av forlengelse av en ellipse oftere uttrykt gjennom eksentrisitet, formelen som er gitt ovenfor. For forskjellige ellipser varierer eksentrisiteten fra 0 til 1, og forblir alltid mindre enn enhet.

Eksempel 3. Komponer den kanoniske ligningen for ellipsen hvis avstanden mellom brennpunktene er 8 og hovedaksen er 10.

Løsning. La oss trekke noen enkle konklusjoner:

Hvis hovedaksen er lik 10, så halvparten av den, dvs. halvaksen en = 5 ,

Hvis avstanden mellom fokusene er 8, så tallet c av fokalkoordinatene er lik 4.

Vi erstatter og beregner:

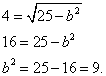
Resultatet er den kanoniske ligningen til ellipsen:

Eksempel 4. Komponer den kanoniske ligningen for en ellipse hvis hovedaksen er 26 og eksentrisiteten er .

Løsning. Som følger av både størrelsen på hovedaksen og eksentrisitetsligningen, ellipsens semimajor akse en= 13. Fra eksentrisitetsligningen uttrykker vi tallet c, nødvendig for å beregne lengden på den mindre halvaksen:

.

Vi beregner kvadratet på lengden av den mindre halvaksen:

Vi komponerer den kanoniske ligningen for ellipsen:

Eksempel 5. Bestem brennpunktene til ellipsen gitt av den kanoniske ligningen.

Løsning. Finn nummeret c, som bestemmer de første koordinatene til ellipsens foci:

.

Vi får fokusene til ellipsen:

Eksempel 6. Fociene til ellipsen er plassert på aksen Okse symmetrisk om opprinnelsen. Komponer den kanoniske ligningen til ellipsen hvis:

1) avstanden mellom fokusene er 30, og hovedaksen er 34

2) mindre akse 24, og ett av fokusene er på punktet (-5; 0)

3) eksentrisitet, og en av fokusene er på punkt (6; 0)

La oss fortsette å løse ellipseproblemer sammen

Hvis er et vilkårlig punkt på ellipsen (angitt med grønt i øvre høyre del av ellipsen på tegningen) og er avstanden til dette punktet fra brennpunktene, så er formlene for avstandene som følger:

For hvert punkt som tilhører ellipsen, er summen av avstandene fra brennpunktene en konstant verdi lik 2 en.

Linjer definert av ligninger

kalles rektorer ellipse (på tegningen er det røde linjer langs kantene).

Fra de to ligningene ovenfor følger det for ethvert punkt på ellipsen

,

hvor og er avstandene til dette punktet til retningslinjene og .

Eksempel 7. Gitt en ellipse. Skriv en ligning for retningene.

Løsning. Vi ser på direktrix-ligningen og finner ut at vi må finne eksentrisiteten til ellipsen, dvs. Vi har alle data for dette. Vi beregner:

.

Vi får ligningen for ellipsens retter:

Eksempel 8. Komponer den kanoniske ligningen til en ellipse hvis fokusene er punkter og retningslinjene er linjer.

(MIF-2, nr. 3, 2005)

Andre ordens linjer på et fly

S. 1. Definisjon av en andre ordrelinje

Tenk på et plan der et rektangulært kartesisk koordinatsystem (XOY) er spesifisert. Da er ethvert punkt M unikt bestemt av dets koordinater (x, y). I tillegg definerer et hvilket som helst tallpar (x, y) et bestemt punkt på planet. Koordinatene til punktene kan tilfredsstille visse betingelser, for eksempel en ligning f(x, y) = 0 med hensyn til de ukjente (x, y). I dette tilfellet sier de at ligningen f(x, y)=0 definerer en viss figur på planet. La oss se på eksempler.

Eksempel 1. Vurder funksjonen y= f( x). Koordinatene til punktene på grafen til denne funksjonen tilfredsstiller ligningen y– f( x) = 0.

Eksempel 2. Ligning (*), hvor en, b, c– noen tall definerer en bestemt rett linje på planet. (Ligninger av formen (*) kalles lineær).

Eksempel 3. Grafen til en hyperbel består av punkter hvis koordinater tilfredsstiller ligningen https://pandia.ru/text/80/134/images/image004_92.gif" width="161" height="25">.

Definisjon 1. Formens ligning (**), hvor minst én av koeffisientene er DIV_ADBLOCK75">

Vi skal se på geometriske og fysiske egenskaper linjene nevnt ovenfor. La oss starte med en ellipse.

https://pandia.ru/text/80/134/images/image008_54.gif" width="79" height="44 src="> (1).

Ligning (1) kalles kanonisk ligningen til en ellipse.

Formen på ellipsen kan bedømmes fra figur 1.

La oss si det. Punktene kalles triks ellipse. Det er en rekke interessante egenskaper knyttet til triks, som vi vil diskutere nedenfor.

Definisjon 4. Hyperbole er en figur på et plan hvis koordinater til alle punktene tilfredsstiller ligningen

(2).

Ligning (2) kalles kanonisk hyperbelligning. Typen hyperbel kan bedømmes fra figur 2.

La oss si det. Punktene kalles triks hyperbole. Parameter en ringte gyldig, og parameteren b- imaginær halvakse hyperbler, henholdsvis okse– ekte, og oh– imaginær akse til hyperbelen.

https://pandia.ru/text/80/134/images/image016_34.gif" width="61" height="41">, kalles asymptoter. For store parameterverdier x punktene til asymptotene nærmer seg grenene til hyperbelen uendelig nært. I figur 2 er asymptotene avbildet med stiplede linjer.

Definisjon 5. En parabel er en figur på et plan hvis koordinater til alle punktene tilfredsstiller ligningen

https://pandia.ru/text/80/134/images/image018_28.gif" width="47" height="45 src=">.

S. 3. Egenskaper til LVP-fokuser

For hver LVP i A.2. spesielle punkter ble angitt - triks. Disse punktene spiller en stor rolle i å forklare de viktige egenskapene til ellipsen, hyperbelen og parabelen. Vi formulerer disse egenskapene i form av teoremer.

Teorem. 1. En ellipse er et sett med punkterM, slik at summen av avstandene fra disse punktene til brennpunktene er lik 2en:

https://pandia.ru/text/80/134/images/image020_26.gif" width="115" height="23 src="> (5).

For å formulere en lignende egenskap for en parabel definerer vi rektor. Det er rett d, gitt av ligningen https://pandia.ru/text/80/134/images/image022_23.gif" width="103" height="21 src="> (6).

S. 4. Fokuser og tangenter

https://pandia.ru/text/80/134/images/image024_24.gif" align="right" width="322" height="386 src=">.gif" width="52" height="24 src="> tilhører den tilsvarende HDL. Nedenfor er ligningene for tangentene som går gjennom dette punktet:

– for en ellipse, (7)

– for hyperbole, (8)

- for en parabel. (9)

Hvis vi tegner segmenter fra begge foci til tangenspunktet med en ellipse eller hyperbel (de kalles fokale radier poeng), så vil noe bemerkelsesverdig bli avslørt eiendom(se fig. 5 og 6): fokale radier danner like vinkler med tangenten tegnet på dette punktet.

Denne egenskapen har en interessant fysisk tolkning. For eksempel, hvis vi anser konturen av en ellipse som speilvendt, da lysstråler fra en punktkilde plassert ved ett fokus, etter refleksjon fra veggene i kretsen, vil nødvendigvis passere gjennom det andre fokuset.

Stor praktisk anvendelse fikk en lignende egenskap for en parabel. Poenget er det brennradiusen til et hvilket som helst punkt i parabelen gjør en vinkel med tangenten trukket til dette punktet lik vinkelen mellom tangenten og aksen til parablen.

Fysisk tolkes dette slik: strålene til et punkt plassert i fokus for parabelen, etter refleksjon fra veggene, forplanter seg parallelt med symmetriaksen til parablen. Derfor har speilene til lykter og spotlights en parabolsk form. Forresten, hvis en strøm av lys (radiobølger) parallelt med parabelens akse kommer inn i den, vil alle strålene etter refleksjon fra veggene passere gjennom fokuset. Romkommunikasjonsstasjoner, så vel som radarer, opererer etter dette prinsippet.

S. 5. Litt mer fysikk

HDL-er har funnet utbredt bruk i fysikk og astronomi. Dermed ble det funnet at ett relativt lett legeme (for eksempel en satellitt) beveger seg i gravitasjonsfeltet til et mer massivt legeme (planet eller stjerne) langs en bane som representerer en av LVP-ene. I dette tilfellet er den mer massive kroppen i fokus for denne banen.

For første gang ble disse egenskapene studert i detalj Johannes Kepler og de ble kalt Keplers lover.

Prøve nr. 1 for 10. klasseelever

Selvtestspørsmål (5 poeng per oppgave)

M.10.1.1. Definer HDL. Gi noen eksempler på ligninger som definerer LVP.

M.10.1.2. Regn ut koordinatene til brennpunktene til a) en ellipse, b) en hyperbel, if en=13, b=5.

M.10.1.3. Komponer den kanoniske ligningen av a) en ellipse, b) en hyperbel, hvis det er kjent at denne linjen går gjennom punkter med koordinater (5, 6) og (-8, 7).

M.10.1.4. Kontroller at den rette linjen gitt av ligning (9) faktisk skjærer parabelen gitt av ligning (3) bare i punktet med koordinater . ( Note: bytt først ut likningen til tangenten i ligningen til parablen, og sørg deretter for at diskriminanten til den resulterende kvadratiske ligningen er null.)

M.10.1.5. Skriv en ligning for tangenten til hyperbelen med reell halvakse 8 og imaginær halvakse – 4 i punktet med koordinat x=11 hvis den andre koordinaten til punktet er negativ.

Praktisk arbeid (10 poeng)

M.10.1.6. Konstruer flere ellipser ved å bruke følgende metode: fest et papirark til kryssfiner og stikk et par knapper inn i papiret (men ikke helt). Ta et stykke tråd og bind endene. Kast den resulterende løkken over begge knappene (fokuspunktene til den fremtidige ellipsen), trekk tråden med den skarpe enden av en blyant og tegn forsiktig en linje, og pass på at tråden er stram. Ved å endre dimensjonene til løkken kan du bygge flere konfokale ellipser. Prøv å forklare ved hjelp av teorem 1 at de resulterende linjene egentlig er ellipser, og forklar hvordan du kan beregne halvaksene til ellipsen ved å vite avstanden mellom knappene og lengden på tråden.

Linjer av andre orden.
Ellipse og dens kanoniske ligning. Sirkel

Etter grundige studier rette linjer i planet Vi fortsetter å studere geometrien til den todimensjonale verden. Innsatsen er doblet, og jeg inviterer deg til å besøke et pittoresk galleri med ellipser, hyperbler, paraboler, som er typiske representanter andre ordens linjer. Ekskursjonen har allerede begynt, og først kort informasjon om hele utstillingen i ulike etasjer i museet:

Konseptet med en algebraisk linje og dens rekkefølge

En linje på et fly kalles algebraisk, hvis i affint koordinatsystem dens ligning har formen , hvor er et polynom som består av termer av formen ( – reelt tall, – ikke-negative heltall).

Som du kan se, inneholder ikke ligningen til en algebraisk linje sinus, cosinus, logaritmer og annen funksjonell beau monde. Bare X og Y er med ikke-negative heltall grader.

Linjebestilling lik maksimalverdien av vilkårene som er inkludert i den.

I følge det tilsvarende teoremet avhenger ikke konseptet med en algebraisk linje, så vel som dens rekkefølge, av valget affint koordinatsystem, derfor, for å lette eksistensen, antar vi at alle etterfølgende beregninger finner sted i Kartesiske koordinater.

Generell ligning den andre ordrelinjen har formen , hvor – vilkårlige reelle tall (Det er vanlig å skrive det med en faktor på to), og koeffisientene er ikke lik null på samme tid.

Hvis , så forenkles ligningen til , og hvis koeffisientene ikke er lik null på samme tid, så er dette nøyaktig generell ligning for en "flat" linje, som representerer første ordrelinje.

Mange har forstått betydningen av de nye begrepene, men likevel, for å mestre materialet 100%, stikker vi fingrene inn i kontakten. For å bestemme linjerekkefølgen, må du iterere alle vilkår dens ligninger og finn for hver av dem summen av grader innkommende variabler.

For eksempel:

begrepet inneholder "x" i 1. potens;
begrepet inneholder "Y" i 1. potens;
Det er ingen variabler i begrepet, så summen av potensene deres er null.

La oss nå finne ut hvorfor ligningen definerer linjen sekund bestille:

begrepet inneholder "x" i 2. potens;
summandet har summen av potensene til variablene: 1 + 1 = 2;
begrepet inneholder "Y" i 2. potens;
alle andre vilkår - mindre grader.

Maksimal verdi: 2

Hvis vi i tillegg legger til, for eksempel, til ligningen vår, vil den allerede bestemme tredje ordens linje. Åpenbart inneholder den generelle formen for 3. ordens linjeligningen et "fullt sett" med termer, summen av potensene til variablene der er lik tre:
, hvor koeffisientene ikke er lik null samtidig.

I tilfelle det legges til ett eller flere passende termer som inneholder , da skal vi allerede snakke om 4. ordens linjer, osv.

Vi vil måtte møte algebraiske linjer av 3., 4. og høyere orden mer enn én gang, spesielt når vi blir kjent med polart koordinatsystem.

La oss imidlertid gå tilbake til den generelle ligningen og huske dens enkleste skolevariasjoner. Som eksempler oppstår en parabel, hvis likning lett kan reduseres til en generell form, og en hyperbel med en ekvivalent likning. Men ikke alt er like glatt...

En betydelig ulempe med den generelle ligningen er at det nesten alltid er uklart hvilken linje den definerer. Selv i det enkleste tilfellet vil du ikke umiddelbart innse at dette er en hyperbole. Slike oppsett er bare gode i en maskerade, så et typisk problem vurderes i løpet av analytisk geometri bringe 2. ordens linjeligningen til kanonisk form.

Hva er den kanoniske formen til en ligning?

Dette er den allment aksepterte standardformen for en ligning, når det i løpet av sekunder blir klart hvilket geometrisk objekt den definerer. I tillegg er den kanoniske formen veldig praktisk for å løse mange praktiske oppgaver. Så for eksempel i henhold til den kanoniske ligningen "flat" rett, for det første er det umiddelbart klart at dette er en rett linje, og for det andre er punktet som tilhører den og retningsvektoren lett synlige.

Det er åpenbart at evt 1. ordrelinje er en rett linje. I andre etasje er det ikke lenger vekteren som venter på oss, men et mye mer mangfoldig selskap med ni statuer:

Klassifisering av andreordens linjer

Ved å bruke et spesielt sett med handlinger, reduseres enhver ligning av en annenordens linje til en av følgende former:

(og er positive reelle tall)

1) – kanonisk ligning av ellipsen;

2) - kanonisk ligning av en hyperbel;

3) – kanonisk ligning av en parabel;

4) – innbilt ellipse;

5) - et par kryssende linjer;

6) – par innbilt kryssende linjer (med et enkelt gyldig skjæringspunkt ved origo);

7) - et par parallelle linjer;

8) – par innbilt parallelle linjer;

9) – et par sammenfallende linjer.

Noen lesere kan ha inntrykk av at listen er ufullstendig. For eksempel, i punkt nr. 7, spesifiserer ligningen paret direkte, parallelt med aksen, og spørsmålet oppstår: hvor er ligningen som bestemmer linjene parallelle med ordinataksen? Svar: det ikke ansett som kanonisk. Rette linjer representerer den samme standardsaken, rotert 90 grader, og tilleggsoppføringen i klassifiseringen er overflødig, siden den ikke gir noe fundamentalt nytt.

Dermed er det ni og bare ni ulike typer linjer av 2. orden, men i praksis finnes de oftest ellipse, hyperbel og parabel.

La oss først se på ellipsen. Som vanlig fokuserer jeg på de punktene som er av stor betydning for å løse problemer, og hvis du trenger en detaljert utledning av formler, bevis på teoremer, vennligst referer for eksempel til læreboken til Bazylev/Atanasyan eller Aleksandrov.

Ellipse og dens kanoniske ligning

Stavemåte ... vennligst ikke gjenta feilene til noen Yandex-brukere som er interessert i "hvordan bygge en ellipse", "forskjellen mellom en ellipse og en oval" og "eksentrisiteten til en ellipse".

Den kanoniske ligningen av en ellipse har formen , hvor er positive reelle tall, og . Jeg vil formulere selve definisjonen av en ellipse senere, men for nå er det på tide å ta en pause fra den snakkende butikken og løse et vanlig problem:

Hvordan bygge en ellipse?

Ja, bare ta det og bare tegne det. Oppgaven forekommer ofte, og en betydelig del av elevene takler ikke tegningen riktig:

Eksempel 1

Konstruer en ellipse, gitt av ligningen

Løsning: Først, la oss bringe ligningen til kanonisk form:

Hvorfor ta med? En av fordelene med den kanoniske ligningen er at den lar deg bestemme umiddelbart toppene av ellipsen, som er plassert på punkter. Det er lett å se at koordinatene til hvert av disse punktene tilfredsstiller ligningen.

I i dette tilfellet :


Segment ringte hovedaksen ellipse;
segment – mindre akse;
tall ringte semi-major skaft ellipse;
tall – mindre akse.
i vårt eksempel: .

For raskt å forestille seg hvordan en bestemt ellipse ser ut, se bare på verdiene til "a" og "be" i dens kanoniske ligning.

Alt er fint, pent og vakkert, men det er ett forbehold: Jeg har laget tegningen ved hjelp av programmet. Og du kan lage tegningen ved å bruke hvilken som helst applikasjon. Men i den harde virkeligheten ligger det et rutete stykke papir på bordet, og mus danser i sirkler på hendene våre. Folk med kunstnerisk talent kan selvfølgelig krangle, men du har også mus (men mindre). Det er ikke forgjeves at menneskeheten oppfant linjalen, kompasset, gradskiven og andre enkle enheter for tegning.

Av denne grunn er det usannsynlig at vi vil være i stand til å tegne en ellipse nøyaktig når vi bare kjenner til toppunktene. Det er greit hvis ellipsen er liten, for eksempel med halvakser. Alternativt kan du redusere skalaen og følgelig dimensjonene på tegningen. Men generelt er det svært ønskelig å finne flere poeng.

Det er to tilnærminger til å konstruere en ellipse - geometrisk og algebraisk. Jeg liker ikke konstruksjon med kompass og linjal fordi algoritmen ikke er den korteste og tegningen er betydelig rotete. I nødstilfeller, vennligst se læreboken, men i virkeligheten er det mye mer rasjonelt å bruke algebraverktøyene. Fra ellipselikningen i utkastet uttrykker vi raskt:

Ligningen deles deretter ned i to funksjoner:
– definerer den øvre buen av ellipsen;
– definerer den nederste buen til ellipsen.

Ellipsen definert av den kanoniske ligningen er symmetrisk med hensyn til koordinataksene, så vel som med hensyn til origo. Og dette er flott - symmetri er nesten alltid en forkynnelse av freebies. Det er åpenbart nok å forholde seg til 1. koordinatkvartal, så vi trenger funksjonen . Det ber om å bli funnet for ytterligere poeng med abscisser . La oss trykke på tre SMS-meldinger på kalkulatoren:

Selvfølgelig er det også fint at hvis det blir gjort en alvorlig feil i beregningene, vil det umiddelbart bli klart under byggingen.

La oss markere punktene på tegningen (rød), symmetriske punkter på de resterende buene (blå) og koble hele selskapet forsiktig med en linje:


Det er bedre å tegne den første skissen veldig tynt, og først deretter bruke press med en blyant. Resultatet skal være en ganske grei ellipse. Vil du forresten vite hva denne kurven er?

Definisjon av en ellipse. Ellipse foci og ellipse eksentrisitet

En ellipse er et spesielt tilfelle av en oval. Ordet "oval" skal ikke forstås i filistinsk betydning ("barnet tegnet en oval", etc.). Dette er et matematisk begrep som har en detaljert formulering. Hensikten med denne leksjonen er ikke å vurdere teorien om ovaler og deres forskjellige typer, som praktisk talt ikke får oppmerksomhet i standardkurset for analytisk geometri. Og, i samsvar med mer aktuelle behov, går vi umiddelbart videre til den strenge definisjonen av en ellipse:

Ellipse er settet av alle punkter i planet, summen av avstandene til hver av dem fra to gitte punkter, kalt triks ellipse, er en konstant størrelse, numerisk lik lengden på hovedaksen til denne ellipsen: .
I dette tilfellet er avstandene mellom fokusene mindre enn denne verdien: .

Nå vil alt bli klarere:

Tenk deg at den blå prikken "reiser" langs en ellipse. Så uansett hvilket punkt på ellipsen vi tar, vil summen av lengdene til segmentene alltid være den samme:

La oss sørge for at i vårt eksempel er verdien av summen virkelig lik åtte. Mentalt plasser punktet "um" ved høyre toppunkt av ellipsen, så: , som er det som måtte sjekkes.

En annen metode for å tegne den er basert på definisjonen av en ellipse. Høyere matematikk er noen ganger årsaken til spenninger og stress, så det er på tide å ha en ny lossingsøkt. Ta whatman-papir eller et stort ark papp og fest det til bordet med to spiker. Dette blir triks. Knyt en grønn tråd til de utstikkende spikerhodene og trekk den hele veien med en blyant. Blyantledningen vil ende opp på et bestemt punkt som hører til ellipsen. Begynn nå å flytte blyanten langs papiret, hold den grønne tråden stram. Fortsett prosessen til du kommer tilbake til utgangspunktet... flott... tegningen kan sjekkes av lege og lærer =)

Hvordan finne brennpunktene til en ellipse?

I eksemplet ovenfor skildret jeg "ferdige" fokuspunkter, og nå skal vi lære å trekke dem ut fra geometriens dybder.

Hvis en ellipse er gitt av en kanonisk ligning, har dens foci koordinater , hvor er dette avstand fra hvert fokus til ellipsens symmetrisenter.

Beregningene er enklere enn enkle:

! De spesifikke koordinatene til foci kan ikke identifiseres med betydningen av "tse"! Jeg gjentar at dette er AVSTAND fra hvert fokus til sentrum(som i det generelle tilfellet ikke trenger å ligge nøyaktig ved origo).
Og derfor kan avstanden mellom foci heller ikke knyttes til den kanoniske posisjonen til ellipsen. Med andre ord kan ellipsen flyttes til et annet sted og verdien vil forbli uendret, mens fokusene vil naturlig endre koordinatene sine. Ta dette i betraktning når du utforsker emnet videre.

Ellipseeksentrisitet og dens geometriske betydning

Eksentrisiteten til en ellipse er et forhold som kan ta verdier innenfor området.

I vårt tilfelle:

La oss finne ut hvordan formen til en ellipse avhenger av dens eksentrisitet. For dette fikse venstre og høyre toppunkt av ellipsen under vurdering, det vil si at verdien av halvhovedaksen vil forbli konstant. Deretter vil eksentrisitetsformelen ha formen: .

La oss begynne å bringe eksentrisitetsverdien nærmere enhet. Dette er bare mulig hvis . Hva betyr det? ...husk triksene . Dette betyr at brennpunktene til ellipsen vil "bevege seg fra hverandre" langs abscisseaksen til sidepunktene. Og siden "de grønne segmentene ikke er gummi", vil ellipsen uunngåelig begynne å flate ut, og bli til en tynnere og tynnere pølse trukket på en akse.

Slik, jo nærmere ellipsens eksentrisitetsverdi er enhet, jo mer langstrakt er ellipsen.

La oss nå modellere den motsatte prosessen: ellipsens foci gikk mot hverandre og nærmet seg sentrum. Dette betyr at verdien av "ce" blir mindre og mindre, og følgelig har eksentrisiteten en tendens til null: .
I dette tilfellet vil de "grønne segmentene" tvert imot "bli overfylte" og de vil begynne å "skyve" ellipselinjen opp og ned.

Slik, Jo nærmere eksentrisitetsverdien er null, jo mer lik er ellipsen... se på det begrensende tilfellet når fokusene er vellykket gjenforent ved opprinnelsen:

En sirkel er et spesielt tilfelle av en ellipse

Faktisk, når det gjelder likestilling av halvaksene, har den kanoniske ligningen av ellipsen formen , som refleksivt transformeres til ligningen av en sirkel med et senter ved opprinnelsen til radius "a", velkjent fra skolen.

I praksis brukes notasjonen med den "talende" bokstaven "er" oftere: . Radius er lengden på et segment, med hvert punkt i sirkelen fjernet fra sentrum med en radiusavstand.

Merk at definisjonen av en ellipse forblir helt korrekt: fociene sammenfaller, og summen av lengdene til de sammenfallende segmentene for hvert punkt på sirkelen er en konstant. Siden avstanden mellom brennpunktene er , da eksentrisiteten til enhver sirkel er null.

Det er enkelt og raskt å konstruere en sirkel, bare bruk et kompass. Noen ganger er det imidlertid nødvendig å finne ut koordinatene til noen av punktene, i dette tilfellet går vi den kjente veien - vi bringer ligningen til den muntre Matanov-formen:

- funksjonen til den øvre halvsirkelen;
– funksjon av den nedre halvsirkelen.

Så finner vi de nødvendige verdiene, differensiere, integrere og gjøre andre gode ting.

Artikkelen er selvfølgelig kun for referanse, men hvordan kan du leve i verden uten kjærlighet? Kreativ oppgave for selvstendig løsning

Eksempel 2

Komponer den kanoniske ligningen til en ellipse hvis en av dens foci og semi-mollakser er kjent (senteret er i origo). Finn hjørner, tilleggspunkter og tegn en linje i tegningen. Beregn eksentrisitet.

Løsning og tegning på slutten av timen

La oss legge til en handling:

Roter og parallelloversetter en ellipse

La oss gå tilbake til den kanoniske ligningen av ellipsen, nemlig til tilstanden hvis mysterium har plaget nysgjerrige sinn siden den første omtalen av denne kurven. Så vi så på ellipsen , men er det ikke mulig i praksis å oppfylle ligningen ? Tross alt, her ser det imidlertid ut til å være en ellipse også!

Denne typen ligninger er sjelden, men den kommer over. Og det definerer faktisk en ellipse. La oss avmystifisere:

Som et resultat av konstruksjonen ble vår opprinnelige ellipse oppnådd, rotert 90 grader. det vil si - Dette ikke-kanonisk oppføring ellipse . Rekord!– ligning definerer ikke noen annen ellipse, siden det ikke er noen punkter (foci) på aksen som vil tilfredsstille definisjonen av en ellipse.

1. Andre ordens linjer på det euklidiske planet.

2. Invarianter av andre ordens linjeligninger.

3. Bestemmelse av typen andreordens linjer fra invariantene til ligningen.

4. Andre ordens linjer på affinplanet. Unikitetsteorem.

5. Sentre av andre ordens linjer.

6. Asymptoter og diametre av andreordens linjer.

7. Redusere ligningene til andreordens linjer til det enkleste.

8. Hovedretninger og diametre av andre ordens linjer.

LISTE OVER BRUKTE REFERANSER

1. Andre ordens linjer i det euklidiske planet.

Definisjon:

Euklidisk fly er et rom med dimensjon 2,

(todimensjonalt reelt rom).

Andreordens linjer er skjæringslinjene for en sirkulær kjegle med plan som ikke passerer gjennom toppunktet.

Disse linjene finnes ofte i ulike naturvitenskapelige spørsmål. For eksempel skjer bevegelsen av et materialpunkt under påvirkning av det sentrale tyngdefeltet langs en av disse linjene.

Hvis skjæreplanet skjærer alle de rettlinjede generatrisene til ett hulrom i kjeglen, vil seksjonen produsere en linje kalt ellipse(Fig. 1.1, a). Hvis skjæreplanet skjærer generatrisene til begge hulrommene i kjeglen, vil seksjonen produsere en linje kalt hyperbole(Fig. 1.1,6). Og til slutt, hvis skjæreplanet er parallelt med en av generatrisene til kjeglen (ved 1.1, V- dette er generatoren AB), da vil seksjonen produsere en linje kalt parabel. Ris. 1.1 gir en visuell representasjon av formen på de aktuelle linjene.

Figur 1.1

Den generelle ligningen for en andreordenslinje er som følger:

(1)

(1*)

Ellipse er settet med punkter på planet der summen av avstandene til tofaste punkterF 1 OgF 2 dette planet, kalt foci, er en konstant verdi.

I dette tilfellet er tilfeldigheten av ellipsens foci ikke utelukket. Åpenbart hvis brennpunktene sammenfaller, så er ellipsen en sirkel.

For å utlede den kanoniske ligningen til ellipsen velger vi origo O til det kartesiske koordinatsystemet i midten av segmentet F 1 F 2 , og øksene Oh Og Oh La oss styre det som vist i fig. 1.2 (hvis triks F 1 Og F 2 sammenfaller, så sammenfaller O med F 1 Og F 2, og for aksen Oh du kan ta hvilken som helst akse som går gjennom OM).

La lengden på segmentet F 1 F 2 F 1 Og F 2 har henholdsvis koordinater (-с, 0) og (с, 0). La oss betegne med 2a konstanten referert til i definisjonen av en ellipse. Åpenbart, 2a > 2c, dvs. a > c ( Hvis M- punkt av ellipsen (se fig. 1.2), deretter | M.F. ] |+ | M.F. 2 | = 2 en, og siden summen av to sider M.F. 1 Og M.F. 2 triangel M.F. 1 F 2 mer tredjepart F 1 F 2 = 2c, deretter 2a > 2c. Det er naturlig å utelukke tilfellet 2a = 2c, siden da punktet M plassert på segmentet F 1 F 2 og ellipsen degenererer til et segment. ).

La M (x, y)(Fig. 1.2). La oss angi avstandene fra punktet med r 1 og r 2 M til poeng F 1 Og F 2 hhv. I henhold til definisjonen av en ellipse likestilling

r 1 + r 2 = 2a(1.1)

er en nødvendig og tilstrekkelig betingelse for plasseringen av punktet M (x, y) på en gitt ellipse.

Ved å bruke formelen for avstanden mellom to punkter får vi

(1.2)

Av (1.1) og (1.2) følger det at forhold

(1.3)

representerer en nødvendig og tilstrekkelig betingelse for plasseringen av et punkt M med koordinatene x og y på en gitt ellipse. Derfor kan relasjon (1.3) betraktes som ellipseligning. Ved å bruke standardmetoden for "ødeleggelse av radikaler" reduseres denne ligningen til formen

(1.4) (1.5)

Siden ligning (1.4) er algebraisk følge ellipseligning (1.3), deretter koordinatene x og y hvilket som helst poeng M ellipse vil også tilfredsstille ligning (1.4). Siden under algebraiske transformasjoner assosiert med å kvitte seg med radikaler, kan "ekstra røtter" dukke opp, må vi sørge for at ethvert punkt M, hvis koordinater tilfredsstiller ligning (1.4), befinner seg på denne ellipsen. For å gjøre dette er det åpenbart nok å bevise at verdiene til r 1 og r 2 for hvert punkt tilfredsstiller relasjonen (1.1). Så la koordinatene X Og på poeng M tilfredsstille ligning (1.4). Erstatter verdien kl 2 fra (1.4) til høyre side av uttrykk (1.2) for r 1, etter enkle transformasjoner finner vi at Ganske likt finner vi at (1.6)

dvs. r 1 + r 2 = 2a, og derfor ligger punktet M på en ellipse. Ligning (1.4) kalles kanonisk ligning av en ellipse. Mengder EN Og b kalles tilsvarende større og mindre halvakser av ellipsen(navnene "stor" og "liten" er forklart av det faktum at a>b).

Kommentar. Hvis halvaksene til ellipsen EN Og b er like, så er ellipsen en sirkel hvis radius er lik R = en = b, og senteret sammenfaller med opprinnelsen.

Hyperbole er settet med punkter på planet som den absolutte verdien av forskjellen i avstander til to faste punkter erF 1 OgF 2 av dette planet, kalt foci, er det en konstant verdi ( Triks F 1 Og F 2 det er naturlig å betrakte hyperbler annerledes, fordi hvis konstanten som er angitt i definisjonen av en hyperbel ikke er lik null, så er det ikke et enkelt punkt på planet hvis de faller sammen F 1 Og F 2 , som ville tilfredsstille kravene til definisjonen av en hyperbel. Hvis denne konstanten er null og F 1 sammenfaller med F 2 , da tilfredsstiller et hvilket som helst punkt på planet kravene til definisjonen av en hyperbel. ).

For å utlede den kanoniske ligningen til en hyperbel, velger vi opprinnelsen til koordinatene i midten av segmentet F 1 F 2 , og øksene Oh Og Oh La oss styre det som vist i fig. 1.2. La lengden på segmentet F 1 F 2 lik 2s. Så i det valgte koordinatsystemet punktene F 1 Og F 2 har henholdsvis koordinater (-с, 0) og (с, 0) La oss betegne med 2 EN konstanten referert til i definisjonen av en hyperbel. Åpenbart 2a< 2с, т. е. en< с.

La M- punkt på flyet med koordinater (x, y)(Fig. 1,2). La oss angi avstandene med r 1 og r 2 M.F. 1 Og M.F. 2 . I henhold til definisjonen av hyperbel likestilling

(1.7)

er en nødvendig og tilstrekkelig betingelse for plassering av punkt M på en gitt hyperbel.

Ved å bruke uttrykk (1.2) for r 1 og r 2 og relasjon (1.7), får vi følgende nødvendig og tilstrekkelig betingelse for plasseringen av et punkt M med koordinatene x og y på en gitt hyperbel:

. (1.8)

Ved å bruke standardmetoden for "ødeleggelse av radikaler", reduserer vi ligning (1.8) til formen

(1.9) (1.10)

Vi må sørge for at likning (1.9), oppnådd ved algebraiske transformasjoner av likning (1.8), ikke har fått nye røtter. For å gjøre dette er det nok å bevise det for hvert punkt M, koordinater X Og på som tilfredsstiller ligning (1.9), tilfredsstiller verdiene av r 1 og r 2 relasjon (1.7). Ved å utføre argumenter som ligner på de som ble laget når vi utledet formler (1.6), finner vi følgende uttrykk for mengdene som er av interesse for oss r 1 og r 2:

(1.11)

Altså for det aktuelle punktet M vi har

, og derfor er den plassert på en hyperbel.

Ligning (1.9) kalles den kanoniske ligningen til en hyperbel. Mengder EN Og b kalles henholdsvis ekte og imaginære halvakser av hyperbelen.

Parabel er settet med punkter på planet som avstanden til et fast punkt er forFdette planet er lik avstanden til en fast rett linje, også plassert i det aktuelle planet.